(프로그래머 | Python/JavaScript) 유한 십진수 결정(입문 코딩 테스트/레벨 0)

by

질문

https://school.programmers.co.kr/learn/courses/30/lessons/120878

프로그램 제작자

'추천 관련글,

코드 중심 개발자를 고용하십시오. 스택 기반 위치 일치. 프로그래머를 위한 개발자별 프로필에 가입하고 기술 호환성이 좋은 회사와 연결하십시오.

프로그래머.co.kr

파이썬
def solution(a, b):
    a_arr = ()
    b_arr = ()
    # 1. 기약분수로 나타내기-분자, 분모의 소인수 확인, 동일한 소인수는 제거
    i = 2
    while a >= i:
        if a % i == 0:
            a //= i
            a_arr.append(i)
        else: 
            i += 1
    i = 2
    while b >= i:
        if b % i == 0:
            b //= i
            if i in a_arr:
                a_arr.remove(i)	#약분
            else:
                b_arr.append(i)
        else: 
            i += 1
    #2. 분모의 소인수가 2와 5인지 확인하기
    for i in b_arr:
        if not i in (2, 5):
            return 2
    return 1

다른 해결 방법

from math import gcd
def solution(a, b):
    b //= gcd(a,b)
    while b % 2==0:
        b //= 2
    while b % 5==0:
        b //= 5
    return 1 if b==1 else 2

gcd()를 사용합니다.

최대 공약수는 기약 분수를 형성하는 데 사용할 수 있습니다.

b(분모)만 풀어야 하므로 2와 5 외에 다른 숫자가 있는지 b만 검사한다.

b를 2와 5로 나눈 나머지가 1이 아닌 경우 b는 2와 5가 아닌 다른 값을 곱한 것이므로 유한하지 않습니다.

def solution(a, b):
    answer = 0
    for i in range(2, min((a, b)) + 1):	#공약수 구해서 a, b에서 나누기(기약분수 만들기)
        while a % i == 0 and b % i == 0:
            a = a // i
            b = b // i
    while b % 2 == 0:
        b = b // 2
    while b % 5 == 0:
        b = b // 5
    if b == 1:
        answer = 1
    else:
        answer = 2
    return answer

gcd()를 사용하지 않는 코드. direct for문을 실행하여 a와 b를 공통인수로 나눈 부분을 제외하면 위의 코드와 논리는 동일합니다.

자바스크립트
function solution(a, b) {
    // 1. 기약분수 만들기
    let gcd = 1;
    for(let i = 2; i <= Math.min(a, b); i++){
        if(a % i === 0 && b % i === 0){
            gcd = i;
        }
    }
    b /= gcd; //공약수로 b 나누기
    // 2. 분모에 2, 5 이외의 숫자가 곱해져 있는지 확인
    while(b % 2 == 0) { b /= 2 };
    while(b % 5 == 0) { b /= 5 };
    return b === 1 ? 1 : 2;
}

파이썬에서 <其他解决方法> GCD를 설명하는 블로그참고용으로 코드를 작성했습니다.

다른 해결 방법

function solution(a, b) {
    return Number((a/b).toFixed(10)) == a/b ? 1 : 2
}

소수점 아래의 숫자가 연속적인지 확인하여 유한 소수를 결정합니다.

소수점 뒤에 연속된 숫자가 있는 경우 무한 소수


고정(N)

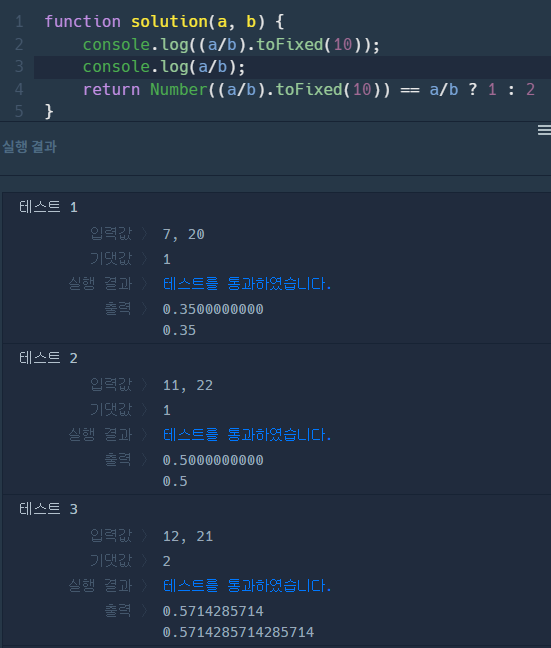
소수점 이하 N 자리까지 정확한 고정 소수점 표기법으로 숫자를 표시하는 방법입니다.


출처: Mozilla.org